DEFINING COMPLEX UNITS

Although MathCAD has over 80 built-in fundamental and derived units, it also allows you to define your own unit. This is extremely useful when working with unusual units found in a particular discipline. When defining a unit, one must be aware the units definition is based entirely on the fundamental units selected and defined by MathCAD. For this example, we will use the English system of units. For the English system, MathCAD uses feet, pound-mass, seconds, Kelvins, coulomb, candela and mole as base units for Length, Mass, Time, Temperature, Charge, Luminosity and Substance (quantity) respectively.

As an example, the velocity of air flow is often determined by measuring the velocity pressure of the air flow using units of inches of water gage, commonly abbreviated as in. w.g. or in. w.c. (water column). The equation relating velocity to velocity pressure is: v.p. = (V/4005)². The velocity V is measured in feet per minute. The constant, 4005, is comprised of a multitude of factors including the density of standard air (68 F), the density of water, acceleration due to gravity, the gravitational constant and basic conversions from feet to inches and minutes to seconds. When doing such a calculation in MathCAD, it would be convenient to be able to display the results in units of in. w.g., but we must first define an inch of water and we must define the units of the constant 4005. Lets take a step by step look at this.

PROBLEM: Determine the velocity pressure of standard air flowing at 1000 FPM. Use proper units.

First, without using units, write the solution to this problem as shown. Variable V is velocity in FPM, Variable vp is velocity pressure in inches of water. This allows us to check the magnitude of the result once we develop our own units.

Lets find the unit associated with the constant 4005. Velocity V has the unit of ft/min. As such, the unit for the constant 4005 must also contain the unit ft/min so as to divide it out. Next, the result of the equation must give us in. w.g. Notice the term V/4005 is squared. This means that in. w.g. must be contained in the denominator of the unit attached to the constant 4005 and it must be held as a square root. The final unit to the constant 4005 would then be ft/min*in_wg^0.5.

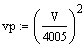
Notice the unit we defined for the constant 4005 now contains the unit in_wg; but in_wg is as yet undefined. To define it, we must understand its derivation.

We first define one foot of water as a pressure that exists at the bottom of a one foot high water column. Water at 60F has a density of 62.33 lb/cf. Let's first determine the specific weight(g).

g = specific weight (lbf/cf)
g=acceleration due to gravity (32.174 ft/sec²)
g_c=gravitational constant (32.174 ft lb/sec² lbf)
r=density (lb/cf)

then:

If this water is contained in a 1' x 1' x 1' cube, we can find the pressure at the bottom of this cube as shown at the right. This calculation is assigned to the variable ft_wg to represent the pressure at the bottom of a one foot column of water. Note the calculation yields the pressure in fundamental units. To see it displayed in psi, substitute psi in the unit placeholder. This results in 0.433 psi/ft w.g. Obviously, 1 in w.g. exerts a pressure equal to 1/12 of that.

Now that the unit, in_wg, is defined, we can rewrite the equation for velocity pressure. The velocity pressure for air at 1000 ft/min is shown; first in its fundamental units, then with our derived unit inserted in the placeholder.

Example: Using the defined unit of in_wg, rearrange the equation to find velocity given a velocity pressure of 0.0842 in w.g.

So as not to have to type out the derived unit for the constant 4005 each time you want to use it, you could define an arbitrary unit, shorter in length, as a substitute. For example, lets define the unit as: .

Now we can use the unit constant in lieu of the derived unit. To rewrite the above example: